Load and Analyze Membrane Potentials and Spike Trains

This example demonstrates post-simulation analysis of the Watanabe and Kohn (2015) spinal network model. It shows how to load chunked simulation data, convert it to NEO format, and analyze membrane potentials, spike trains, and population dynamics.

Note

Analysis workflow:

1. Load simulation parameters from previous run

2. Convert chunked data to NEO Block format (compatible with all analysis tools)

3. Analyze membrane potentials for representative motor neurons

4. Generate spike raster plots showing recruitment patterns

5. Compute population firing rates across simulation phases

6. Save visualizations for publication

Important

Prerequisites: This example requires simulation output from:

• Run 03_10pct_mvc_simulation.py first

• Generates chunked data in results/watanabe_chunks/

• Creates simulation parameters in results/watanabe_simulation_params.pkl

Key Features:

• Chunked data loading: Efficient memory usage for long simulations (15+ seconds)

• NEO format conversion: Seamless compatibility with existing analysis pipelines

• Three-phase analysis: Separate visualization of constant and modulated drive phases

• Publication-quality plots: Membrane potentials, spike rasters, population rates

MyoGen Components Used:

• convert_chunks_to_neo(): Converts chunked simulation data back into a standard NEO Block. This is the recommended way to load large simulation results.

External Libraries Used:

• NEO (neo.Block, neo.Segment, neo.SpikeTrain, neo.AnalogSignal): Standardized format for electrophysiology data. MyoGen uses NEO throughout for interoperability with analysis tools like Elephant, SpyKING CIRCUS, etc.

• joblib: Fast serialization for saving/loading large Python objects.

Data Structures Explained:

• neo.Block: Top-level container holding multiple segments (experimental trials)

• neo.Segment: One recording session containing spike trains and analog signals

• neo.SpikeTrain: Spike times for one neuron with metadata (units, t_stop, etc.)

• neo.AnalogSignal: Continuous data (e.g., membrane potential) with sampling rate

Use Case: Analyze motor unit recruitment, synchronization, and firing patterns to validate model predictions against experimental data from Watanabe and Kohn (2015).

Workflow Position: Step 4 of 6

Next Step: Run 05_compute_force_from_spinal_network.py to generate force output.

Import Libraries

from pathlib import Path

import joblib
import matplotlib.pyplot as plt
import numpy as np

from myogen.utils.continuous_saver import convert_chunks_to_neo

plt.style.use("fivethirtyeight")

# Get colors 1, 2, 3 from the style color cycle for the three phases
phase_colors = plt.rcParams["axes.prop_cycle"].by_key()["color"][1:4]

Load Simulation Parameters

Load the parameters from the simulation to ensure analysis matches the actual run

try:
    _script_dir = Path(__file__).parent
except NameError:
    _script_dir = Path.cwd()

results_path = _script_dir / "results"
params_file = results_path / "watanabe_simulation_params.pkl"

if not params_file.exists():
    raise FileNotFoundError(
        f"Simulation parameters file not found: {params_file}\n"
        "Please run 03_10pct_mvc_simulation.py first to generate the simulation data."
    )

sim_params = joblib.load(params_file)
segment_duration__s = sim_params["segment_duration__s"]
tstop__ms = sim_params["tstop__ms"]
dt__ms = sim_params["dt__ms"]

print("=" * 70)
print("SIMULATION PARAMETERS")
print("=" * 70)
print(f"Segment duration: {segment_duration__s} s")
print(f"Total duration: {tstop__ms / 1000} s ({tstop__ms} ms)")
print(f"Timestep: {dt__ms} ms")
print(f"Motor neurons: {sim_params['naMN']}")

# Calculate phase boundaries
phase1_end = segment_duration__s
phase2_end = 2 * segment_duration__s
phase3_end = 3 * segment_duration__s

======================================================================
SIMULATION PARAMETERS
======================================================================
Segment duration: 5 s
Total duration: 15.0 s (15000.0 ms)
Timestep: 0.025 ms
Motor neurons: 800

Load Data as NEO Block

This is the RECOMMENDED approach - converts chunks to a NEO Block that’s identical in structure to what SimulationRunner.run() returns

chunks_path = results_path / "watanabe_chunks"

print("=" * 70)
print("LOADING SIMULATION DATA AS NEO BLOCK")
print("=" * 70)
print(f"Chunks directory: {chunks_path}\n")

# Convert chunks to NEO Block format (compatible with SimulationRunner output)
# All data (spikes + membrane potentials) is self-contained in the chunks
results = convert_chunks_to_neo(chunks_path)

print("\nNEO Block loaded successfully!")
print(f"\tType: {type(results)}")
print(f"\tSegments: {len(results.segments)}")

for seg in results.segments:
    print(
        f"\t{seg.name}: {len(seg.spiketrains)} spike trains, "
        f"\t{len(seg.analogsignals)} analog signals"
    )

======================================================================
LOADING SIMULATION DATA AS NEO BLOCK
======================================================================
Chunks directory: /home/runner/work/MyoGen/MyoGen/examples/03_papers/watanabe/results/watanabe_chunks

Converting chunks to NEO Block format...
  Loading spike data from: /home/runner/work/MyoGen/MyoGen/examples/03_papers/watanabe/results/watanabe_chunks/spikes.pkl
        Duration: 14999.975000312128 ms
        Timestep: 0.025 ms
        Total chunks: 3
        Adding spike trains...

        Creating DD spike trains:   0%|          | 0/400 [00:00<?, ?it/s]
        Creating DD spike trains:  24%|██▍       | 95/400 [00:00<00:00, 944.42it/s]
        Creating DD spike trains:  48%|████▊     | 190/400 [00:00<00:00, 942.34it/s]
        Creating DD spike trains:  71%|███████▏  | 285/400 [00:00<00:00, 931.36it/s]
        Creating DD spike trains:  95%|█████████▍| 379/400 [00:00<00:00, 933.29it/s]

        DD: 400 spike trains

        Creating IN spike trains:   0%|          | 0/800 [00:00<?, ?it/s]
        Creating IN spike trains:   7%|▋         | 57/800 [00:00<00:01, 564.95it/s]
        Creating IN spike trains:  14%|█▍        | 115/800 [00:00<00:01, 567.99it/s]
        Creating IN spike trains:  22%|██▏       | 172/800 [00:00<00:01, 567.91it/s]
        Creating IN spike trains:  29%|██▊       | 229/800 [00:00<00:01, 566.76it/s]
        Creating IN spike trains:  36%|███▌      | 286/800 [00:00<00:00, 564.99it/s]
        Creating IN spike trains:  43%|████▎     | 343/800 [00:00<00:00, 565.65it/s]
        Creating IN spike trains:  50%|█████     | 400/800 [00:00<00:00, 565.53it/s]
        Creating IN spike trains:  57%|█████▋    | 457/800 [00:00<00:00, 565.33it/s]
        Creating IN spike trains:  64%|██████▍   | 514/800 [00:00<00:00, 564.74it/s]
        Creating IN spike trains:  71%|███████▏  | 571/800 [00:01<00:00, 563.76it/s]
        Creating IN spike trains:  78%|███████▊  | 628/800 [00:01<00:00, 561.78it/s]
        Creating IN spike trains:  86%|████████▌ | 685/800 [00:01<00:00, 559.86it/s]
        Creating IN spike trains:  93%|█████████▎| 741/800 [00:01<00:00, 559.71it/s]
        Creating IN spike trains: 100%|█████████▉| 797/800 [00:01<00:00, 559.79it/s]

        IN: 800 spike trains

        Creating aMN spike trains:   0%|          | 0/671 [00:00<?, ?it/s]
        Creating aMN spike trains:  15%|█▍        | 100/671 [00:00<00:00, 990.84it/s]
        Creating aMN spike trains:  30%|██▉       | 200/671 [00:00<00:00, 988.54it/s]
        Creating aMN spike trains:  45%|████▍     | 299/671 [00:00<00:00, 981.51it/s]
        Creating aMN spike trains:  59%|█████▉    | 398/671 [00:00<00:00, 977.40it/s]
        Creating aMN spike trains:  74%|███████▍  | 496/671 [00:00<00:00, 973.51it/s]
        Creating aMN spike trains:  89%|████████▊ | 594/671 [00:00<00:00, 970.72it/s]

        aMN: 671 spike trains
        Loading and combining membrane data from 3 chunks...
        aMN: Combining 160 neurons from 3 chunks...

        Loading aMN chunks:   0%|          | 0/3 [00:00<?, ?chunk/s]
        Loading aMN chunks:  33%|███▎      | 1/3 [00:01<00:03,  1.52s/chunk]
        Loading aMN chunks:  67%|██████▋   | 2/3 [00:03<00:01,  1.54s/chunk]
        Loading aMN chunks: 100%|██████████| 3/3 [00:04<00:00,  1.54s/chunk]
        Loading aMN chunks: 100%|██████████| 3/3 [00:04<00:00,  1.54s/chunk]
        aMN: Creating analog signals...

        Creating aMN signals:   0%|          | 0/160 [00:00<?, ?signal/s]
        Creating aMN signals:  24%|██▍       | 39/160 [00:00<00:00, 388.92signal/s]
        Creating aMN signals:  49%|████▉     | 79/160 [00:00<00:00, 393.83signal/s]
        Creating aMN signals:  74%|███████▍  | 119/160 [00:00<00:00, 395.39signal/s]
        Creating aMN signals:  99%|█████████▉| 159/160 [00:00<00:00, 392.96signal/s]

        aMN: 160 analog signals created

NEO Block created successfully
        Total segments: 3

NEO Block loaded successfully!
        Type: <class 'neo.core.block.Block'>
        Segments: 3
        DD: 400 spike trains,   0 analog signals
        IN: 800 spike trains,   0 analog signals
        aMN: 671 spike trains,  160 analog signals

Analyze Membrane Potentials

Access membrane potentials from NEO AnalogSignals

print("\n" + "=" * 70)
print("ANALYZING MEMBRANE POTENTIALS")
print("=" * 70)

# Find the aMN segment
aMN_segment = None
for seg in results.segments:
    if seg.name == "aMN":
        aMN_segment = seg
        break

if aMN_segment and len(aMN_segment.analogsignals) > 0:
    # Extract analog signals
    analog_signals = aMN_segment.analogsignals
    n_neurons = len(analog_signals)

    # Get time vector from first signal
    first_signal = analog_signals[0]
    times_ms = first_signal.times.rescale("ms").magnitude
    sampling_period = float(first_signal.sampling_period.rescale("ms"))

    print("\nMembrane potential recording:")
    print("\tPopulation: aMN (alpha motor neurons)")
    print(f"\tRecorded neurons: {n_neurons}")
    print(f"\tTime range: {times_ms[0]:.1f} - {times_ms[-1]:.1f} ms")
    print(f"\tDuration: {(times_ms[-1] - times_ms[0]) / 1000:.1f} seconds")
    print(f"\tSampling period: {sampling_period} ms")
    print(f"\tSamples per neuron: {len(times_ms)}")

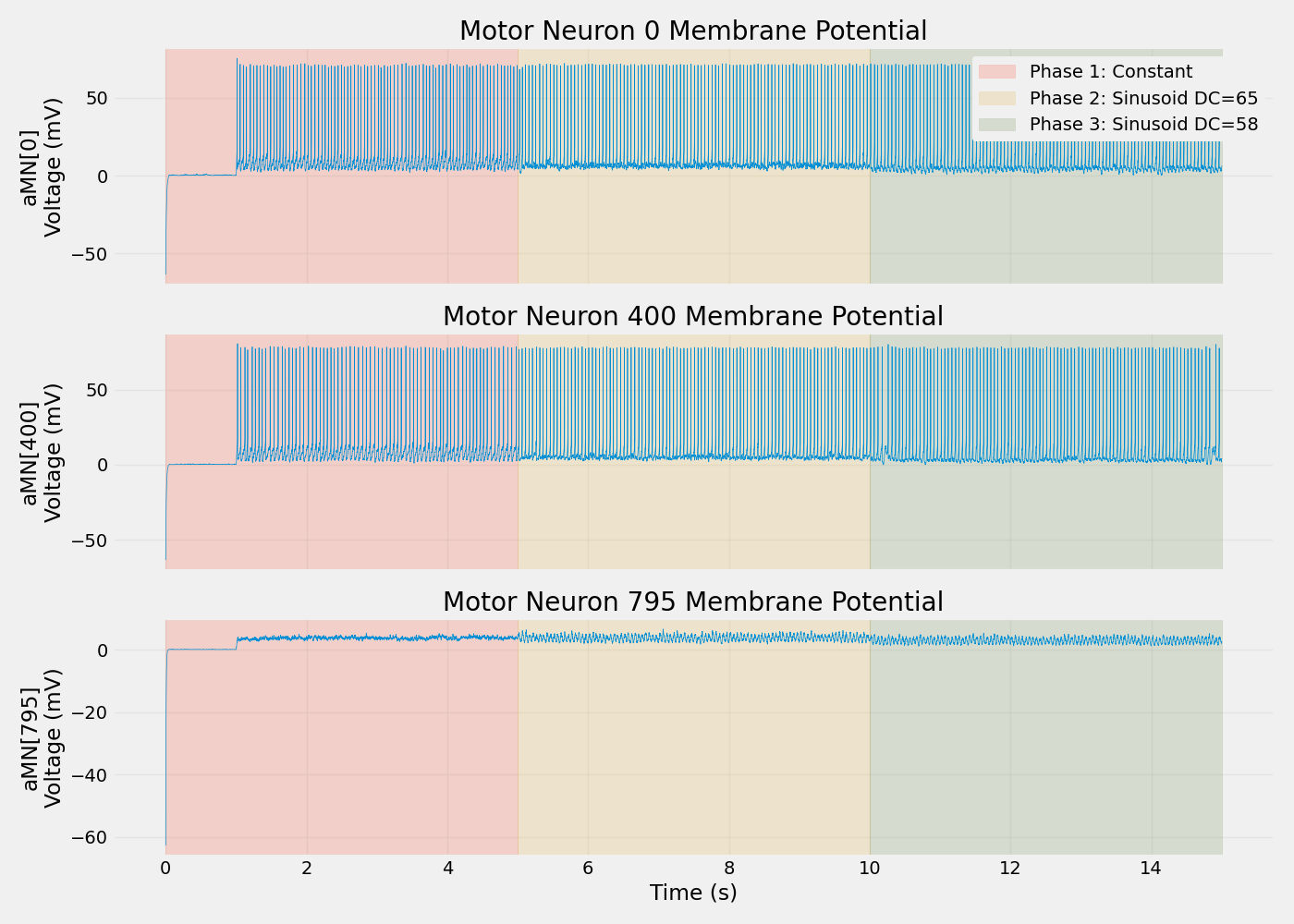
    # Plot membrane potentials for early, middle, and late recruited neurons
    fig, axes = plt.subplots(3, 1, figsize=(14, 10), sharex=True)

    # Select neurons to plot
    indices_to_plot = [0, n_neurons // 2, n_neurons - 1]

    for ax, idx in zip(axes, indices_to_plot):
        signal = analog_signals[idx]
        neuron_id = signal.name  # Actual neuron ID
        voltage = signal.rescale("mV").magnitude.flatten()

        ax.plot(times_ms / 1000.0, voltage, linewidth=0.5)
        ax.set_ylabel(f"aMN[{neuron_id}]\nVoltage (mV)")
        ax.set_title(f"Motor Neuron {neuron_id} Membrane Potential")
        ax.grid(True, alpha=0.3)

        # Highlight the three experimental phases
        ax.axvspan(0, phase1_end, alpha=0.2, color=phase_colors[0], label="Phase 1: Constant")
        ax.axvspan(
            phase1_end,
            phase2_end,
            alpha=0.2,
            color=phase_colors[1],
            label="Phase 2: Sinusoid DC=65",
        )
        ax.axvspan(
            phase2_end,
            phase3_end,
            alpha=0.2,
            color=phase_colors[2],
            label="Phase 3: Sinusoid DC=58",
        )

        if ax == axes[0]:
            ax.legend(loc="upper right", framealpha=1.0, edgecolor="none")

    axes[-1].set_xlabel("Time (s)")
    plt.tight_layout()
    plt.savefig(
        chunks_path.parent / "watanabe_membrane_potentials.png", dpi=150, bbox_inches="tight"
    )
    print(f"\n(OK) Saved plot: {chunks_path.parent / 'watanabe_membrane_potentials.png'}")
    plt.show()

======================================================================
ANALYZING MEMBRANE POTENTIALS
======================================================================

Membrane potential recording:
        Population: aMN (alpha motor neurons)
        Recorded neurons: 160
        Time range: 0.0 - 15000.0 ms
        Duration: 15.0 seconds
        Sampling period: 0.025 ms
        Samples per neuron: 600000

(OK) Saved plot: /home/runner/work/MyoGen/MyoGen/examples/03_papers/watanabe/results/watanabe_membrane_potentials.png

Analyze Spike Data Summary

Print summary statistics for all neural populations

print("\n" + "=" * 70)
print("ANALYZING SPIKE DATA")
print("=" * 70)

# Print summary for all populations
for seg in results.segments:
    if len(seg.spiketrains) > 0:
        n_units = len(seg.spiketrains)
        n_spikes = sum(len(st) for st in seg.spiketrains)
        duration_s = float(seg.spiketrains[0].t_stop.rescale("s"))

        print(f"\n\t{seg.name}:")
        print(f"\t\tTotal units: {n_units}")
        print(f"\t\tTotal spikes: {n_spikes}")
        if duration_s > 0 and n_units > 0:
            print(f"\t\tMean firing rate: {n_spikes / n_units / duration_s:.2f} Hz")

======================================================================
ANALYZING SPIKE DATA
======================================================================

        DD:
                Total units: 400
                Total spikes: 209307
                Mean firing rate: 34.88 Hz

        IN:
                Total units: 800
                Total spikes: 1497311
                Mean firing rate: 124.78 Hz

        aMN:
                Total units: 671
                Total spikes: 152422
                Mean firing rate: 15.14 Hz

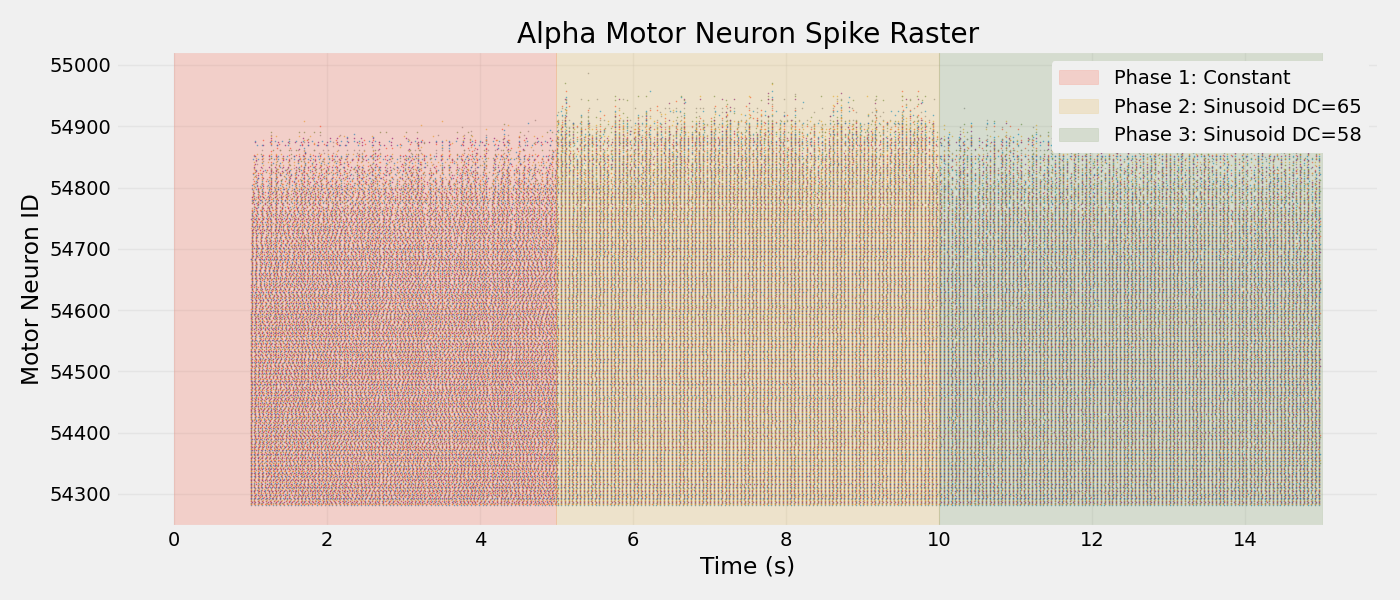
Generate Spike Raster Plot

Visualize spike timing across all motor neurons with phase highlighting

# Plot raster plot for aMN population
if aMN_segment and len(aMN_segment.spiketrains) > 0:
    print("\n" + "=" * 70)
    print("GENERATING SPIKE RASTER PLOT")
    print("=" * 70)

    fig, ax = plt.subplots(figsize=(14, 6))

    # Extract spike times and IDs from NEO spike trains
    for st in aMN_segment.spiketrains:
        neuron_id = int(st.name)
        spike_times_s = st.times.rescale("s").magnitude
        if len(spike_times_s) > 0:
            ax.scatter(
                spike_times_s,
                [neuron_id] * len(spike_times_s),
                s=0.5,
                alpha=0.5,
            )

    ax.set_xlabel("Time (s)")
    ax.set_ylabel("Motor Neuron ID")
    ax.set_title("Alpha Motor Neuron Spike Raster")
    ax.grid(True, alpha=0.3)

    # Highlight the three experimental phases
    ax.axvspan(0, phase1_end, alpha=0.2, color=phase_colors[0], label="Phase 1: Constant")
    ax.axvspan(
        phase1_end, phase2_end, alpha=0.2, color=phase_colors[1], label="Phase 2: Sinusoid DC=65"
    )
    ax.axvspan(
        phase2_end, phase3_end, alpha=0.2, color=phase_colors[2], label="Phase 3: Sinusoid DC=58"
    )
    ax.legend(loc="upper right", framealpha=1.0, edgecolor="none")

    plt.tight_layout()
    plt.savefig(chunks_path.parent / "watanabe_spike_raster.png", dpi=150, bbox_inches="tight")
    print(f"(OK) Saved plot: {chunks_path.parent / 'watanabe_spike_raster.png'}")
    plt.show()

======================================================================
GENERATING SPIKE RASTER PLOT
======================================================================
(OK) Saved plot: /home/runner/work/MyoGen/MyoGen/examples/03_papers/watanabe/results/watanabe_spike_raster.png

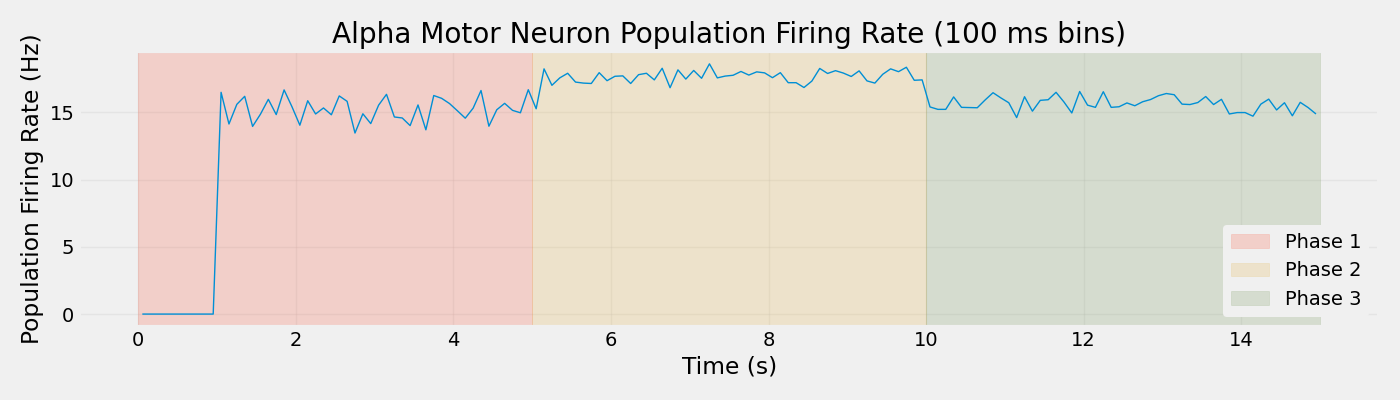
Analyze Population Firing Rate

Compute and visualize population-level firing rate dynamics over time

if aMN_segment and len(aMN_segment.spiketrains) > 0:
    print("\n" + "=" * 70)
    print("GENERATING POPULATION FIRING RATE PLOT")
    print("=" * 70)

    fig, ax = plt.subplots(figsize=(14, 4))

    # Collect all spike times
    all_spike_times = []
    for st in aMN_segment.spiketrains:
        all_spike_times.extend(st.times.rescale("ms").magnitude)
    all_spike_times = np.array(all_spike_times)

    # Calculate population firing rate in 100 ms bins
    bin_size_ms = 100
    duration_ms = float(aMN_segment.spiketrains[0].t_stop.rescale("ms"))
    bins = np.arange(0, duration_ms + bin_size_ms, bin_size_ms)
    counts, _ = np.histogram(all_spike_times, bins=bins)

    # Convert to firing rate (spikes/sec/neuron)
    n_neurons = len(aMN_segment.spiketrains)
    firing_rate = counts / (bin_size_ms / 1000.0) / n_neurons
    bin_centers = (bins[:-1] + bins[1:]) / 2

    ax.plot(bin_centers / 1000.0, firing_rate, linewidth=1)
    ax.set_xlabel("Time (s)")
    ax.set_ylabel("Population Firing Rate (Hz)")
    ax.set_title(f"Alpha Motor Neuron Population Firing Rate ({bin_size_ms} ms bins)")
    ax.grid(True, alpha=0.3)

    # Highlight the three experimental phases
    ax.axvspan(0, phase1_end, alpha=0.2, color=phase_colors[0], label="Phase 1")
    ax.axvspan(phase1_end, phase2_end, alpha=0.2, color=phase_colors[1], label="Phase 2")
    ax.axvspan(phase2_end, phase3_end, alpha=0.2, color=phase_colors[2], label="Phase 3")
    ax.legend(framealpha=1.0, edgecolor="none")

    plt.tight_layout()
    plt.savefig(chunks_path.parent / "watanabe_firing_rate.png", dpi=150, bbox_inches="tight")
    print(f"(OK) Saved plot: {chunks_path.parent / 'watanabe_firing_rate.png'}")
    plt.show()

======================================================================
GENERATING POPULATION FIRING RATE PLOT
======================================================================
(OK) Saved plot: /home/runner/work/MyoGen/MyoGen/examples/03_papers/watanabe/results/watanabe_firing_rate.png

Save NEO Block for Future Use (OPTIONAL)

# NOTE: Saving the full NEO Block is slow (~23 GB of data) and unnecessary
# since we can quickly regenerate it from chunks using convert_chunks_to_neo()
#
# If you really want to save it, uncomment below and use compress=0 for speed:
#
print("\nSaving NEO Block for future use...")

neo_output_path = chunks_path.parent / "watanabe_results_neo.pkl"
joblib.dump(results, neo_output_path, compress=0)  # No compression = faster
print(f"(OK) NEO Block saved to: {neo_output_path}")

Saving NEO Block for future use...
(OK) NEO Block saved to: /home/runner/work/MyoGen/MyoGen/examples/03_papers/watanabe/results/watanabe_results_neo.pkl