Cortical Inputs and Motor Unit Spike Trains

Instead of using injected currents, we can simulate the spike trains of the motor units by using cortical inputs.

Note

The spike trains are simulated using the NEURON simulator wrapped by PyNN. This way we can simulate accurately the biophysical properties of the motor units.

Import Libraries

Important

In MyoGen all random number generation is handled by the RANDOM_GENERATOR object.

This object is a wrapper around the numpy.random module and is used to generate random numbers.

It is intended to be used with the following API:

from myogen import simulator, RANDOM_GENERATOR

To change the default seed, use set_random_seed:

from myogen import set_random_seed
set_random_seed(42)

from pathlib import Path

import joblib
from myogen.utils.currents import create_trapezoid_current
import numpy as np
from matplotlib import pyplot as plt

from myogen import simulator, RANDOM_GENERATOR
from myogen.utils import load_nmodl_files
from myogen.utils.cortical_inputs import create_sinusoidal_cortical_input
from myogen.utils.plotting import plot_spike_trains

Define Parameters

In this example we will simulate a motor pool using the recruitment thresholds generated in the previous example.

This motor pool will have two different randomly generated trapezoidal ramp currents injected into the motor units.

The parameters of the input current are:

• n_pools: Number of distinct motor neuron pools

• timestep: Simulation timestep in ms (high resolution)

• simulation_time: Total simulation duration in ms

To simulate realistic spike trains, we will also add a common noise current source to each neuron. The parameters of the noise current are:

• noise_mean: Mean noise current in nA

• noise_stdev: Standard deviation of noise current in nA

n_pools = 2  # Number of distinct motor neuron pools

timestep = 0.05  # Simulation timestep in ms (high resolution)
simulation_time = 2000  # Total simulation duration in ms

noise_mean = 26  # Mean noise current in nA
noise_stdev = 20  # Standard deviation of noise current in nA

Create Cortical Inputs

To drive the motor units, we use cortical inputs.

In this example, we use a sinusoidal input firing rate which is generated using the create_sinusoidal_cortical_input function.

Note

More convenient functions for generating input current profiles are available in the myogen.utils.cortical_inputs module.

# Calculate number of time points
t_points = int(simulation_time / timestep)

# Generate random parameters for each pool's cortical input
amplitude_range = list(RANDOM_GENERATOR.uniform(20, 80, size=n_pools))
offsets = list(RANDOM_GENERATOR.uniform(50, 100, size=n_pools))
frequencies = list(RANDOM_GENERATOR.uniform(0.5, 10, size=n_pools))
phases = list(RANDOM_GENERATOR.uniform(0, 2 * np.pi, size=n_pools))

CST_number = 400
connection_prob = 0.3


print(f"\nCortical inputs parameters:")
for i in range(n_pools):
    print(
        f"  Pool {i + 1}: amplitude={amplitude_range[i]:.1f} pps, "
        f"offset={offsets[i]:.1f} pps, "
        f"frequency={frequencies[i]:.1f} Hz, "
        f"phase={phases[i]:.1f} rad"
    )

# Create the cortical input matrix
cortical_input__matrix = create_sinusoidal_cortical_input(
    n_pools,
    t_points,
    timestep,
    amplitudes__pps=amplitude_range,
    frequencies__Hz=frequencies,
    offsets__pps=offsets,
    phases__rad=phases,
)

print(
    f"\nCortical input matrix shape: {cortical_input__matrix.shape}\n amplitude={amplitude_range[i]:.1f} pps \n offset={offsets[i]:.1f} pps\n frequency={frequencies[i]:.1f} Hz\nphase={phases[i]:.1f} rad"
)

Cortical inputs parameters:
  Pool 1: amplitude=73.7 pps, offset=98.7 pps, frequency=5.4 Hz, phase=2.3 rad
  Pool 2: amplitude=68.0 pps, offset=83.9 pps, frequency=4.1 Hz, phase=0.8 rad

Cortical input matrix shape: (2, 40000)
 amplitude=68.0 pps
 offset=83.9 pps
 frequency=4.1 Hz
phase=0.8 rad

Create Motor Neuron Pools

Since the recruitment thresholds are already generated, we can load them from the previous example using joblib.

Afterwards the custom files made for the NEURON simulator must be loaded.

Note

This step is required as NEURON does not support the simulation of motor units directly.

This is done using the load_nmodl_files function.

Finally, the motor neuron pools are created using the MotorNeuronPool object.

Note

The MotorNeuronPool object handles the simulation of the motor units.

save_path = Path("./results")

# Load recruitment thresholds
recruitment_thresholds = joblib.load(save_path / "thresholds.pkl")


# Load NEURON mechanism
load_nmodl_files()

# Create motor neuron pool
motor_neuron_pool = simulator.MotorNeuronPool(recruitment_thresholds)

# Compute MVC current threshold
mvc_current_threshold = motor_neuron_pool.mvc_current_threshold

print(f"\nMVC current threshold: {mvc_current_threshold:.1f} nA")

NMODL mechanisms appear to already be loaded, skipping reload

Creating motor neuron pools:   0%|          | 0/1 [00:00<?, ?pool/s]
Creating motor neuron pools: 100%|██████████| 1/1 [00:00<00:00, 24.65pool/s]

Injecting currents into pools:   0%|          | 0/1 [00:00<?, ?pool/s]

Adding noise to neurons in pool:   0%|          | 0/100 [00:00<?, ?neuron/s]


Injecting currents into pools: 100%|██████████| 1/1 [00:00<00:00, 30.84pool/s]

Creating motor neuron pools:   0%|          | 0/1 [00:00<?, ?pool/s]
Creating motor neuron pools: 100%|██████████| 1/1 [00:00<00:00, 24.36pool/s]

Injecting currents into pools:   0%|          | 0/1 [00:00<?, ?pool/s]

Adding noise to neurons in pool:   0%|          | 0/100 [00:00<?, ?neuron/s]


Injecting currents into pools: 100%|██████████| 1/1 [00:00<00:00, 31.67pool/s]

Creating motor neuron pools:   0%|          | 0/1 [00:00<?, ?pool/s]
Creating motor neuron pools: 100%|██████████| 1/1 [00:00<00:00, 23.98pool/s]

Injecting currents into pools:   0%|          | 0/1 [00:00<?, ?pool/s]

Adding noise to neurons in pool:   0%|          | 0/100 [00:00<?, ?neuron/s]


Injecting currents into pools: 100%|██████████| 1/1 [00:00<00:00, 31.46pool/s]

Creating motor neuron pools:   0%|          | 0/1 [00:00<?, ?pool/s]
Creating motor neuron pools: 100%|██████████| 1/1 [00:00<00:00, 23.88pool/s]

Injecting currents into pools:   0%|          | 0/1 [00:00<?, ?pool/s]

Adding noise to neurons in pool:   0%|          | 0/100 [00:00<?, ?neuron/s]


Injecting currents into pools: 100%|██████████| 1/1 [00:00<00:00, 31.45pool/s]

Creating motor neuron pools:   0%|          | 0/1 [00:00<?, ?pool/s]
Creating motor neuron pools: 100%|██████████| 1/1 [00:00<00:00, 24.05pool/s]

Injecting currents into pools:   0%|          | 0/1 [00:00<?, ?pool/s]

Adding noise to neurons in pool:   0%|          | 0/100 [00:00<?, ?neuron/s]


Injecting currents into pools: 100%|██████████| 1/1 [00:00<00:00, 31.31pool/s]

Creating motor neuron pools:   0%|          | 0/1 [00:00<?, ?pool/s]
Creating motor neuron pools: 100%|██████████| 1/1 [00:00<00:00, 24.20pool/s]

Injecting currents into pools:   0%|          | 0/1 [00:00<?, ?pool/s]

Adding noise to neurons in pool:   0%|          | 0/100 [00:00<?, ?neuron/s]


Injecting currents into pools: 100%|██████████| 1/1 [00:00<00:00, 31.17pool/s]

Creating motor neuron pools:   0%|          | 0/1 [00:00<?, ?pool/s]
Creating motor neuron pools: 100%|██████████| 1/1 [00:00<00:00, 24.42pool/s]

Injecting currents into pools:   0%|          | 0/1 [00:00<?, ?pool/s]

Adding noise to neurons in pool:   0%|          | 0/100 [00:00<?, ?neuron/s]


Injecting currents into pools: 100%|██████████| 1/1 [00:00<00:00, 31.16pool/s]

Creating motor neuron pools:   0%|          | 0/1 [00:00<?, ?pool/s]
Creating motor neuron pools: 100%|██████████| 1/1 [00:00<00:00, 24.65pool/s]

Injecting currents into pools:   0%|          | 0/1 [00:00<?, ?pool/s]

Adding noise to neurons in pool:   0%|          | 0/100 [00:00<?, ?neuron/s]


Injecting currents into pools: 100%|██████████| 1/1 [00:00<00:00, 31.43pool/s]

Creating motor neuron pools:   0%|          | 0/1 [00:00<?, ?pool/s]
Creating motor neuron pools: 100%|██████████| 1/1 [00:00<00:00, 24.20pool/s]

Injecting currents into pools:   0%|          | 0/1 [00:00<?, ?pool/s]

Adding noise to neurons in pool:   0%|          | 0/100 [00:00<?, ?neuron/s]


Injecting currents into pools: 100%|██████████| 1/1 [00:00<00:00, 31.01pool/s]

Creating motor neuron pools:   0%|          | 0/1 [00:00<?, ?pool/s]
Creating motor neuron pools: 100%|██████████| 1/1 [00:00<00:00, 24.62pool/s]

Injecting currents into pools:   0%|          | 0/1 [00:00<?, ?pool/s]

Adding noise to neurons in pool:   0%|          | 0/100 [00:00<?, ?neuron/s]


Injecting currents into pools: 100%|██████████| 1/1 [00:00<00:00, 31.34pool/s]

Creating motor neuron pools:   0%|          | 0/1 [00:00<?, ?pool/s]
Creating motor neuron pools: 100%|██████████| 1/1 [00:00<00:00, 24.78pool/s]

Injecting currents into pools:   0%|          | 0/1 [00:00<?, ?pool/s]

Adding noise to neurons in pool:   0%|          | 0/100 [00:00<?, ?neuron/s]


Injecting currents into pools: 100%|██████████| 1/1 [00:00<00:00, 31.73pool/s]

MVC current threshold: 305.7 nA

Simulate Motor Unit Spike Trains

The motor unit spike trains are simulated using the generate_spike_trains method of the MotorNeuronPool object.

spike_trains_matrix, active_neuron_indices, data = (
    motor_neuron_pool.generate_spike_trains(
        cortical_input__matrix=cortical_input__matrix,
        timestep__ms=timestep,
        CST_number=CST_number,
        connection_prob=connection_prob,
    )
)


# Save motor neuron pool for later analysis
joblib.dump(motor_neuron_pool, save_path / "motor_neuron_pool.pkl")

print(f"\nSpike trains shape: {spike_trains_matrix.shape}")
print(f"  - {spike_trains_matrix.shape[0]} pools")
print(f"  - {spike_trains_matrix.shape[1]} neurons per pool")
print(f"  - {spike_trains_matrix.shape[2]} time points\n")

Creating motor neuron pools:   0%|          | 0/2 [00:00<?, ?pool/s]
Creating motor neuron pools: 100%|██████████| 2/2 [00:00<00:00, 24.80pool/s]

Spike trains shape: (2, 100, 40000)
  - 2 pools
  - 100 neurons per pool
  - 40000 time points

Calculate and Display Statistics

It might be of interest to calculate the firing rates of the motor units.

Note

The firing rates are calculated as the number of spikes divided by the simulation time. The simulation time is in milliseconds, so we need to convert it to seconds.

# Calculate firing rates for each pool
firing_rates = np.zeros((n_pools, len(motor_neuron_pool.recruitment_thresholds)))
for pool_idx in range(n_pools):
    for neuron_idx in range(len(motor_neuron_pool.recruitment_thresholds)):
        spike_count = np.sum(spike_trains_matrix[pool_idx, neuron_idx, :])
        firing_rates[pool_idx, neuron_idx] = spike_count / (simulation_time / 1000.0)

print(f"\nFiring rate statistics:")
for pool_idx in range(n_pools):
    active_neurons = np.sum(firing_rates[pool_idx, :] > 0)
    mean_rate = np.mean(firing_rates[pool_idx, firing_rates[pool_idx, :] > 0])
    max_rate = np.max(firing_rates[pool_idx, :])

    print(
        f"  Pool {pool_idx + 1}: {active_neurons}/{len(motor_neuron_pool.recruitment_thresholds)} active neurons, "
        f"mean rate: {mean_rate:.1f} Hz, max rate: {max_rate:.1f} Hz"
    )

Firing rate statistics:
  Pool 1: 100/100 active neurons, mean rate: 29.7 Hz, max rate: 52.0 Hz
  Pool 2: 100/100 active neurons, mean rate: 25.6 Hz, max rate: 47.5 Hz

Visualize Spike Trains

The spike trains can be visualized using the plot_spike_trains function.

Note

Plotting helper functions are available in the myogen.utils.plotting module.

from myogen.utils.plotting import plot_spike_trains

# Suppress font warnings to keep output clean
import warnings
import logging

warnings.filterwarnings("ignore", message=".*Font family.*not found.*")
warnings.filterwarnings("ignore", message=".*findfont.*")
logging.getLogger("matplotlib.font_manager").setLevel(logging.ERROR)

print("Plotting spike trains...")
with plt.xkcd():
    _, ax = plt.subplots(figsize=(10, 6))
    plot_spike_trains(
        spike_trains__matrix=spike_trains_matrix,
        timestep__ms=timestep,
        axs=[ax],
        cortical_input__matrix=cortical_input__matrix,
        pool_to_plot=[0],
    )
plt.tight_layout()
plt.show()

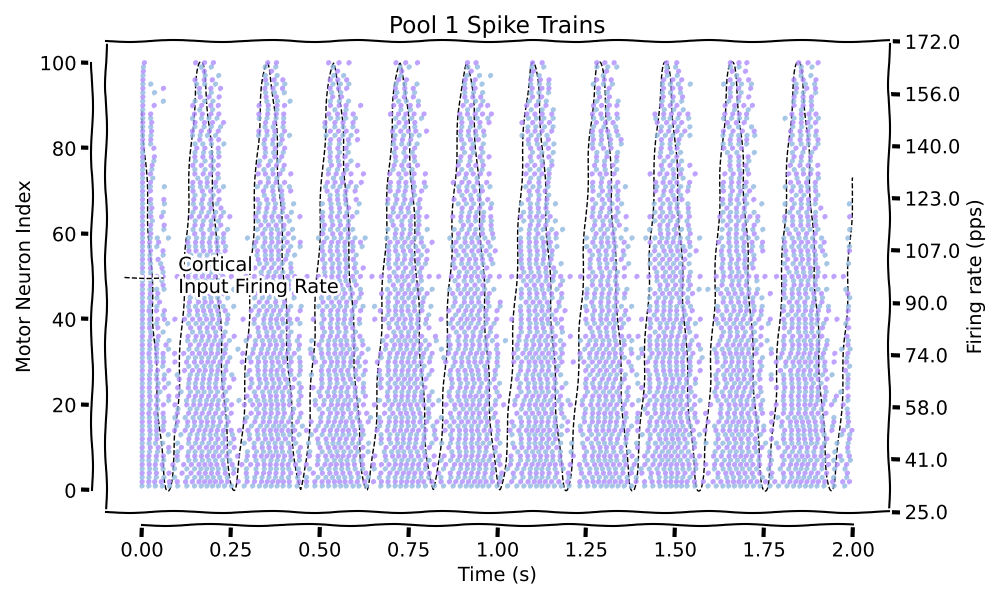
Plotting spike trains...
24.957624733696136 172.3773978363144
index 100